Introduction

The knight's travails problem is a classic interview question where you must find the shortest path for a knight to travel from one square of a chessboard to another. I came across it while working my way through The Odin Project's JavaScript curriculum and really enjoyed the challenge it provided.

The Problem

Given two positions on a chessboard, build a function that shows the shortest possible way for a knight to get from one square to the other. Here’s an example of input and output:

knightMoves([3,3],[0,0]) == [[3,3],[1,2],[0,0]]

Solution

To solve this problem, I chose to represent the chessboard as a graph using an adjacency list. Each vertex in the graph represents a square on the board, and each edge represents a valid move the knight can make from one square to another.

I implemented the adjacency list using a Map object with an array of two coordinates for each key.

Implementing a Graph in JavaScript

const SIZE = 8
const chessboard = new Map()

// Add Vertices. Creates a set of all possible chess positions. '0, 0' => []
for (let i = 0; i < SIZE; i++) {
  for (let j = 0; j < SIZE; j++) {
    chessboard.set(`${[i, j]}`, [])
  }
}

I did run into some issues comparing equality between arrays within the Map object. As you can see above my workaround was to make the keys strings instead of integer arrays. If I were to come back to the problem I would use another data structure. In this case, however, I was happy to gain some experience using a Map.

With the graph in place, I did some Googling on graph search algorithms and compared depth-first to breadth-first algorithms. A breadth-first search (BFS) seemed to be the most appropriate for this problem.

A BFS will begin by adding every edge of a vertex to a queue. Then it will repeat the process for each of those vertices, adding each additional edge to the queue if it hasn’t already been visited. This way we can slowly branch out from our starting position on the chessboard, carving paths in every direction until the end position is reached. A depth first algorithm would begin carving unnecessarily long paths for this problem.

To start, I parsed the key of each square into separate integer variables. Then, I declared a list of operations for each move. Finally, I added an adjacency list of all possible moves for each vertex in the map object.

// Parse x, y coordinates of each vertex as integers for arithmetic
for (let [square] of chessboard) {
  const x = parseInt(square[0]) // x
  const y = parseInt(square[2]) // y

  // A list of operations to simulate all moves
  const options = [
    [x + 1, y + 2],
    [x + 2, y + 1],
    [x + 2, y - 1],
    [x + 1, y - 2],
    [x - 1, y - 2],
    [x - 2, y - 1],
    [x - 2, y + 1],
    [x - 1, y + 2],
  ]

  // Add Edges. Adds an adjacency list of all possible moves from each vertex. '0, 0' => ['1, 2', '2, 1']
  options.forEach((option) => {
    const move = option.toString()
    if (chessboard.has(move)) chessboard.get(square).push(move)
  })
}

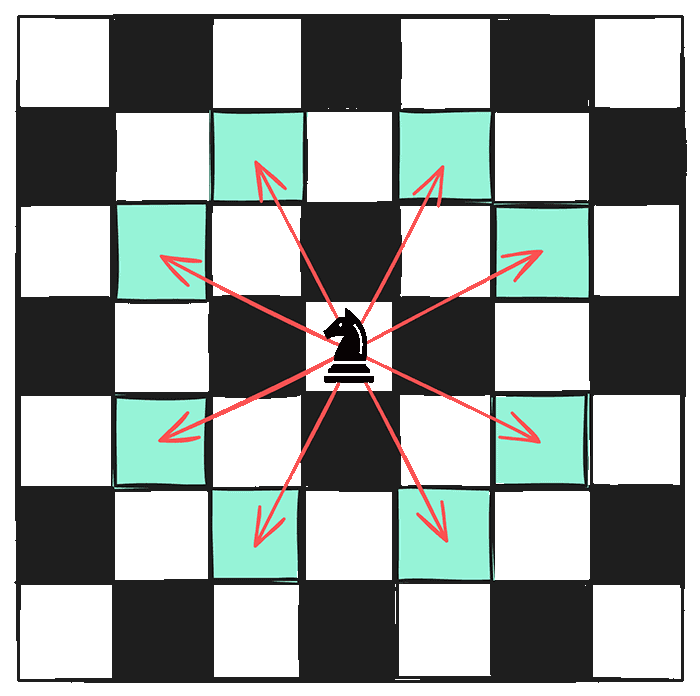
Using a Queue to Find the Shortest Path

To implement the breadth-first search algorithm, I used a queue data structure to keep track of the next vertices to visit. We start with the source vertex and add it to the queue. Then, we visit each of its neighbors and add them one by one to the queue. As vertices are removed from the queue, they are added to a set of visited squares. This ensures that we don't visit the same vertex twice. This process continues until we reach the destination vertex.

Once we've found the destination vertex, we have all the breadcrumbs needed to return the shortest path. It's quite easy in this case. Since we are using a BFS, the first path to reach the target will be the shortest one.

Here's the code I ended up with:

// Find the shortest path from start to end. Time complexity: O(V+E)
function knightMoves(start, end) {
  const queue = []
  const visited = new Set()

  queue.push([start.toString(), [start.toString()]]) // -> ['x, y', ['x, y']]

  while (queue.length > 0) {
    let [currentPosition, path] = queue.shift()
    visited.add(currentPosition)

    // Terminal condition
    if (currentPosition === end.toString()) {
      return printResult(path)
    }

    const possibleMoves = chessboard.get(currentPosition) // -> ['4,2', '3,3', ...]

    for (let move of possibleMoves) {
      if (!visited.has(move)) queue.push([move, [...path, move]])
      console.log(queue)
      // queue -> ['4,2', ['0,0', '2,1', '4,2']]
    }
  }
  return 0
}

// Print result to console, called when the algorithm is finished
const printResult = (path) => {
  console.log(`=> You made it in ${path.length - 1} moves! Here's your path:`)
  path.forEach((move) => {
    console.log(`[${move}]`)
  })
}

Time Complexity and Improvements

The time complexity of this algorithm is O(V + E), where V is the number of vertices and E is the number of edges. In this case, V is the number of squares on the board (64), and E is the sum total of possible knight moves from each square (up to a maximum of 8 per square), which is 336.

While this algorithm is efficient for small chessboards, it quickly becomes impractical for larger boards. One improvement would be to use a bidirectional search to simultaneously search from the source and destination vertices. This would significantly reduce the search space and improve the algorithm's time complexity.

Takeaway

I'm sure there are better ways to implement this, but I'm happy with this solution. I learned a lot about graph traversal. With some improvements, this algorithm can be scaled to solve larger chessboards.